Sample-efficient Bayesian optimisation
using known invariances

Neural Information Processing Systems, 2024

Theo Brown

theo.brown@ukaea.uk

UK Atomic Energy Authority

University College London

Alexandru Cioba

alexandru.cioba@mtkresearch.com

MediaTek Research

Ilija Bogunovic

i.bogunovic@ucl.ac.uk

University College London

Bayesian optimisation

Wide range of applications

Nuclear fusion reactors
[Proxima Fusion]

Goal: sample efficiency

Symmetry and invariance

How can we exploit symmetry in BO?

Objective function is known to be symmetric
Key insight: making one observation gives additional information
In the noiseless case, this is perfect information

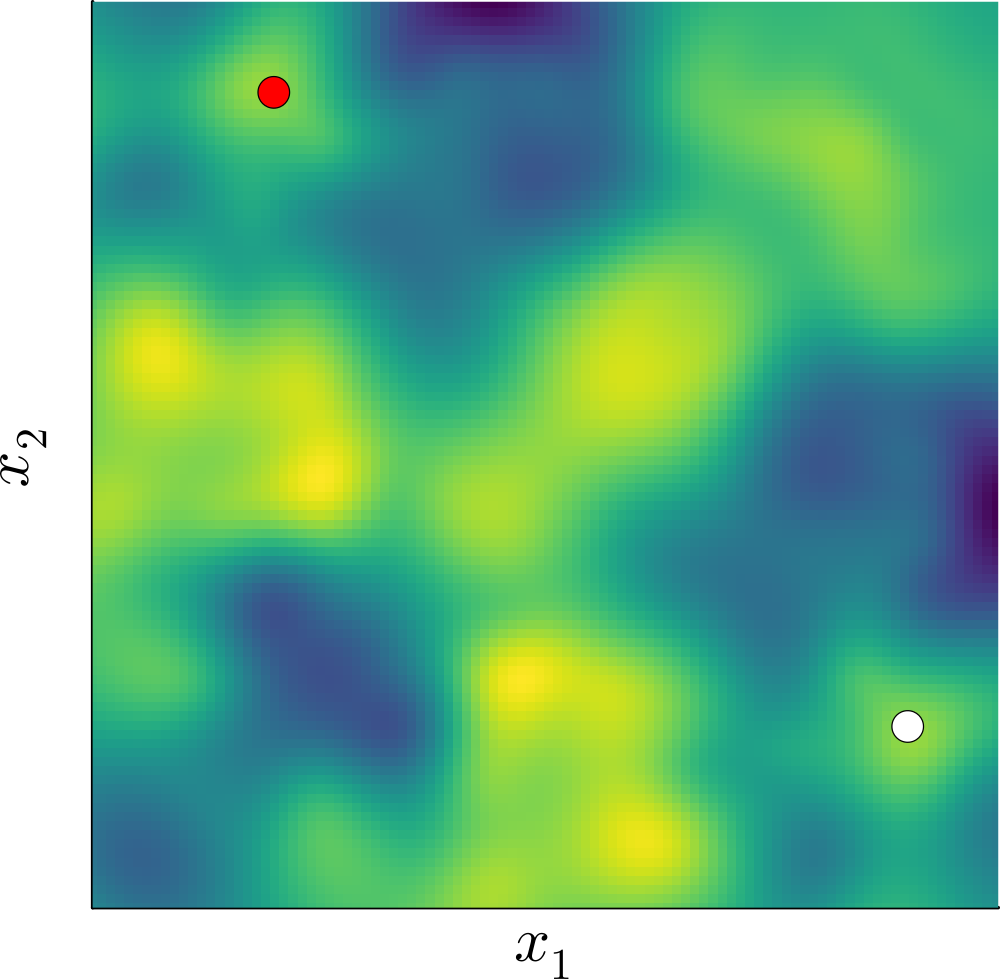
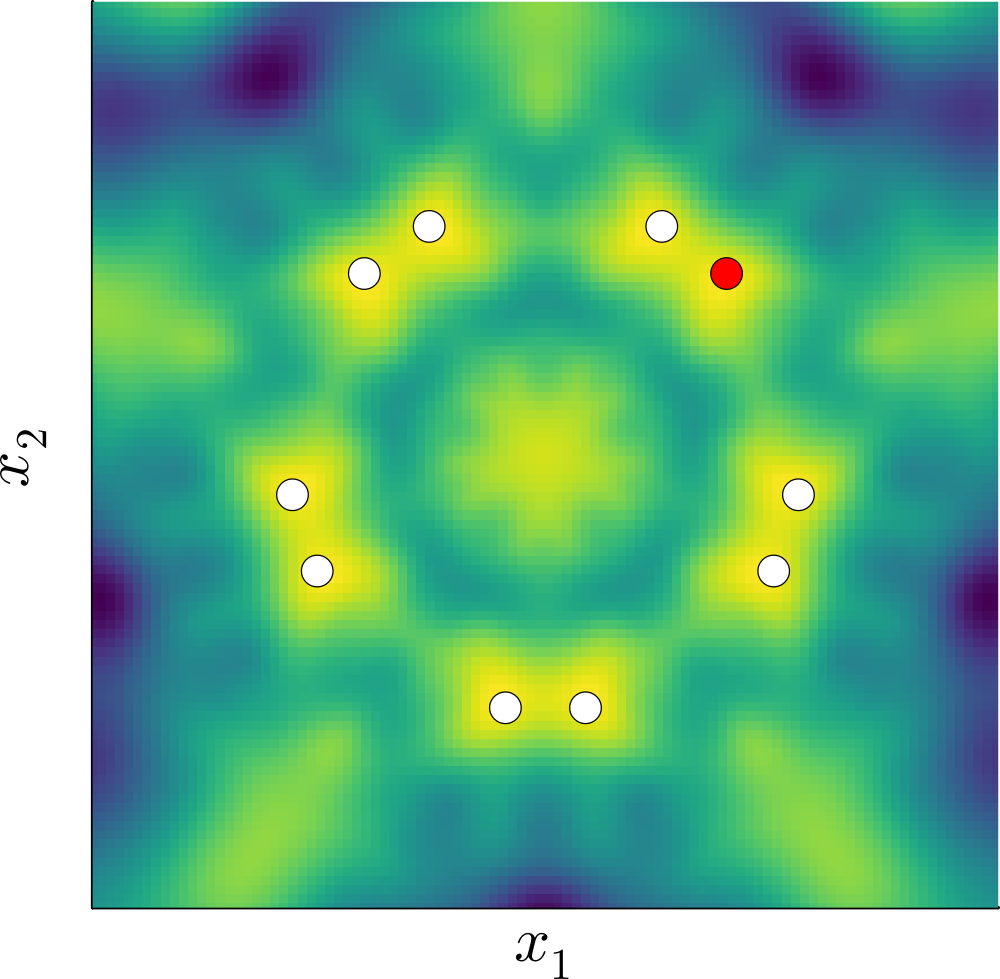
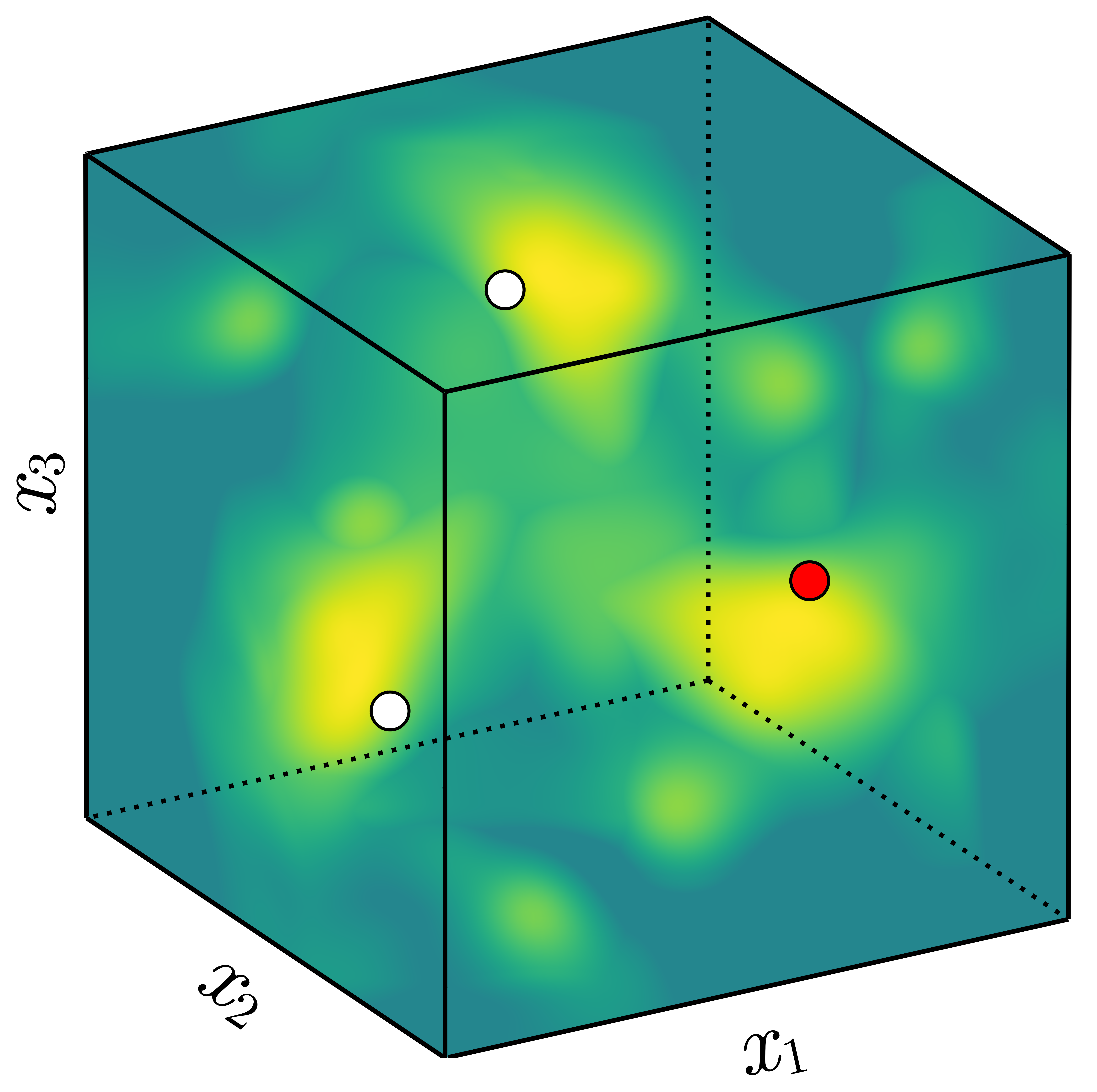
Invariant Gaussian processes

Naive method: data augmentation

Key insight: making one observation gives additional information

Data augmentation: add transformed data to dataset \[ \mathcal{D} \gets \mathcal{D} \cup \{(\sigma(x), f(x)) \quad \forall \sigma \in G, x \in \mathcal{D}\} \]

Problem: computational cost of GP scales with \(\mathcal{O}(\textcolor{#9a2515}{|G|^3} n^3)\)

Can we do better?

Invariant Gaussian processes

Our method: invariant kernel

Construct an invariant kernel: \[ k_G(x, x') = \frac{1}{|G|} \sum_{\sigma \in G} k(x, \sigma(x')) \]

GPs with this kernel are distributions over invariant functions!

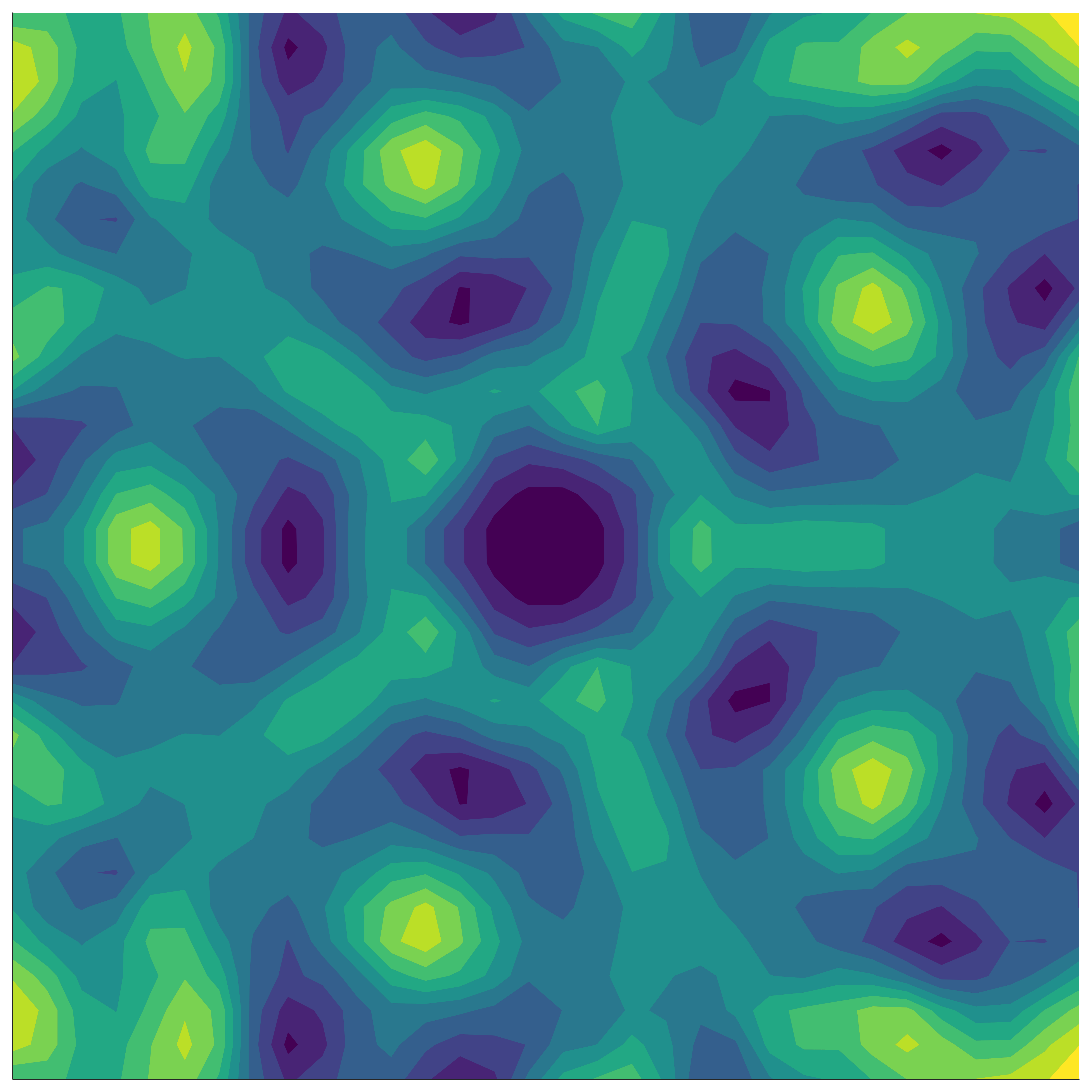
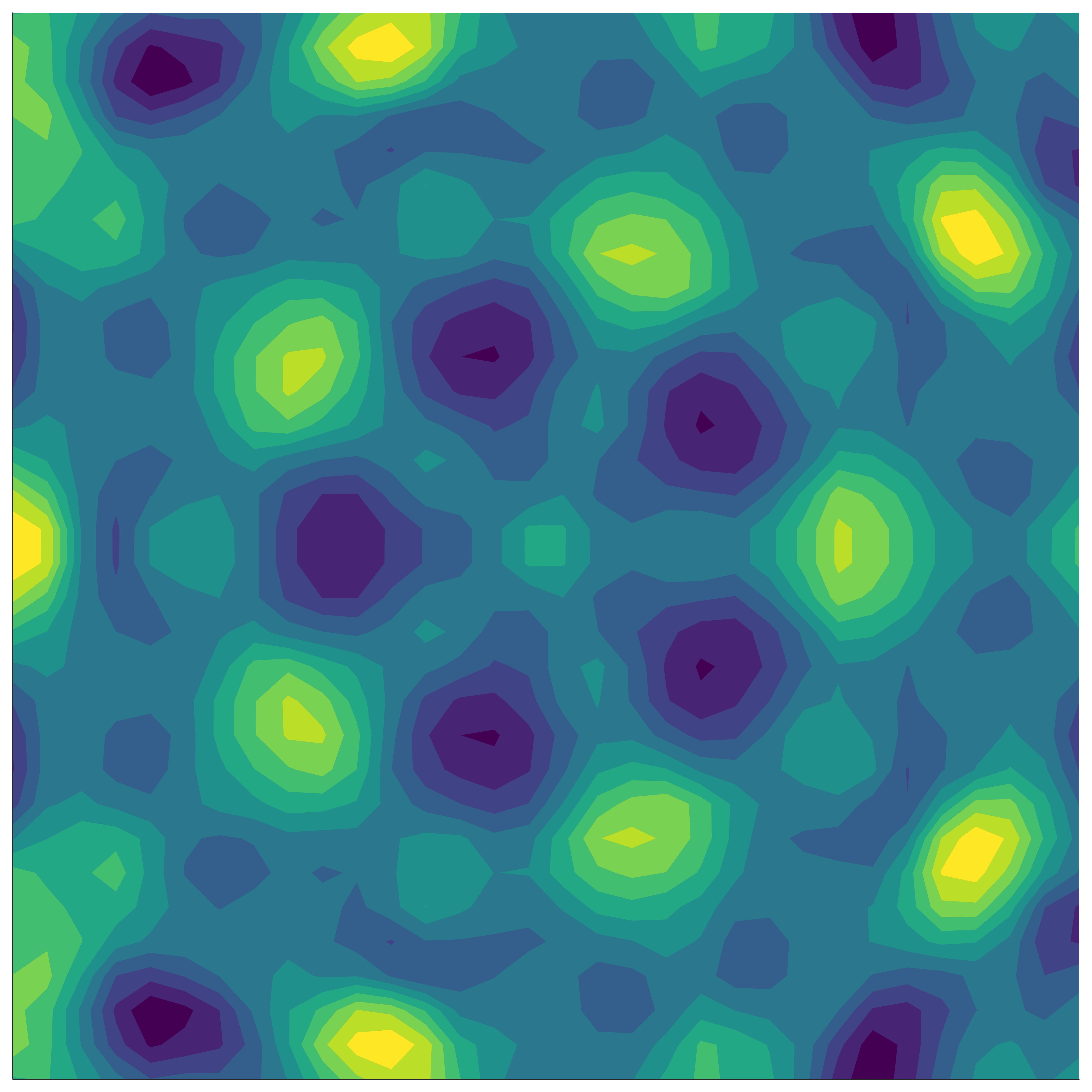
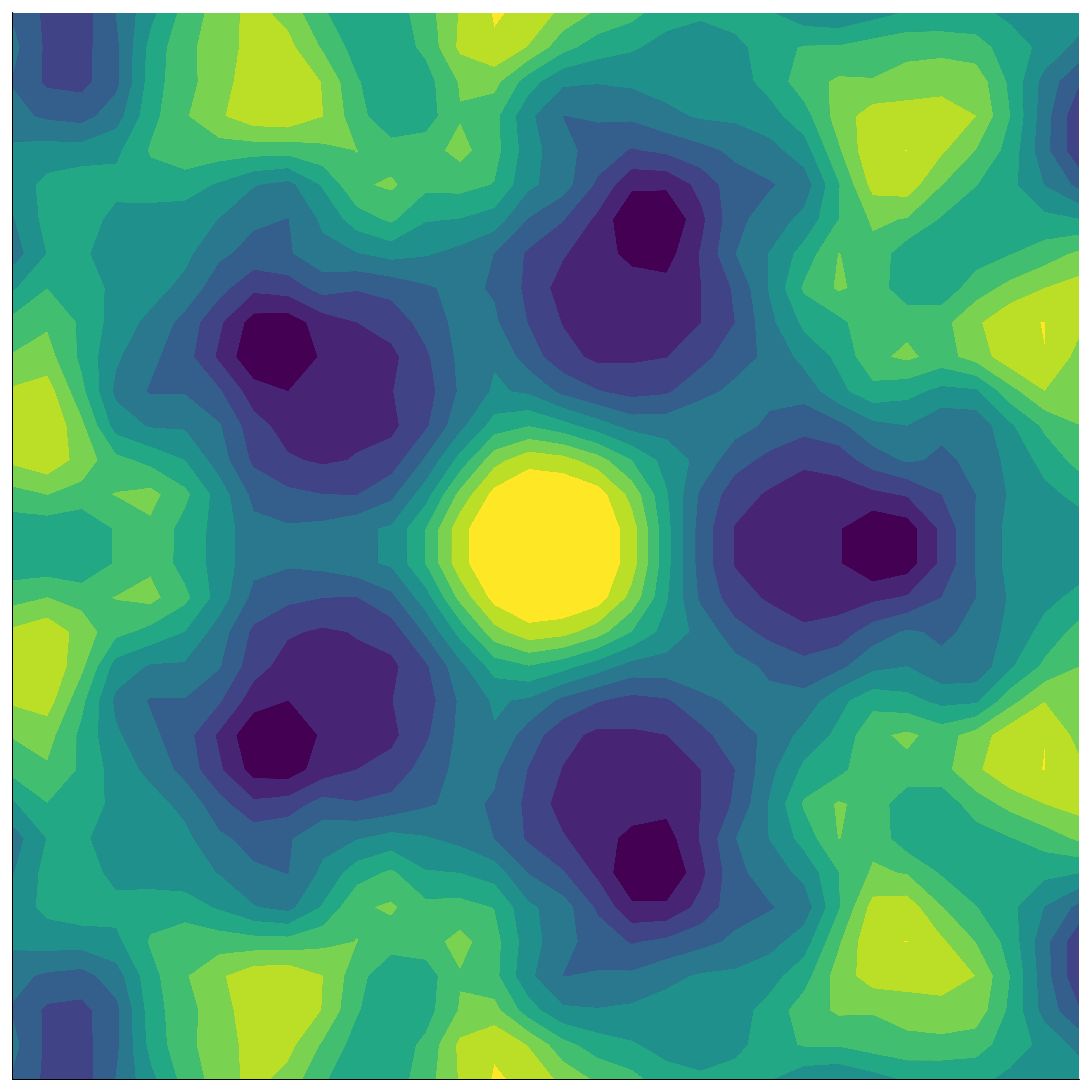
Compute cost reduced from \(\mathcal{O}(\textcolor{#9a2515}{|G|^3} n^3)\) to \(\mathcal{O}(\textcolor{#259a15}{|G|} n^3)\)

Sample complexity for invariant kernel BO

Number of samples \(T\) for precision \(\epsilon\)

Our upper bound:

\[\begin{align} T = \tilde{\mathcal{O}}\left( \left( {\textcolor{#259a15}{\frac{1}{|G|}}} \right)^\frac{2\nu + d -1}{2 \nu} \epsilon^{-\frac{2\nu + d -1}{\nu}} \right) \end{align}\]

Large \(|G|\) → large reduction in number of samples
Lower bound in our paper

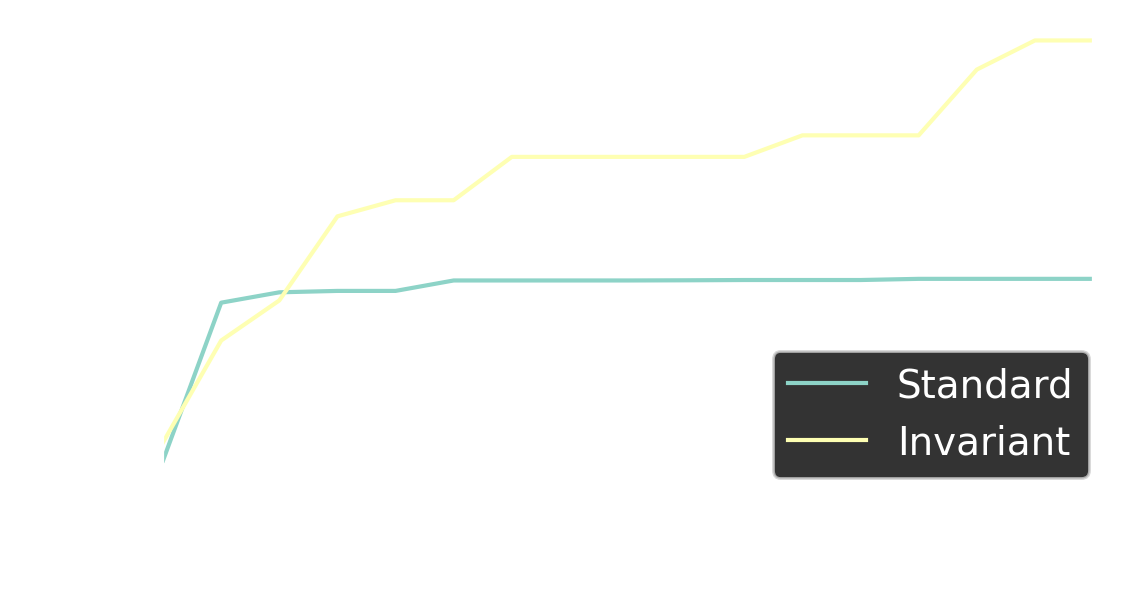
Synthetic experiments

Invariant GP-MVR

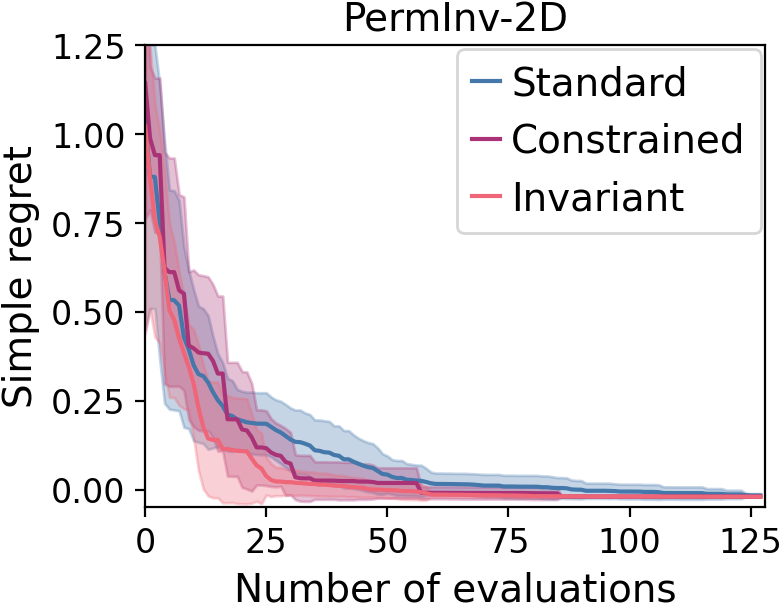
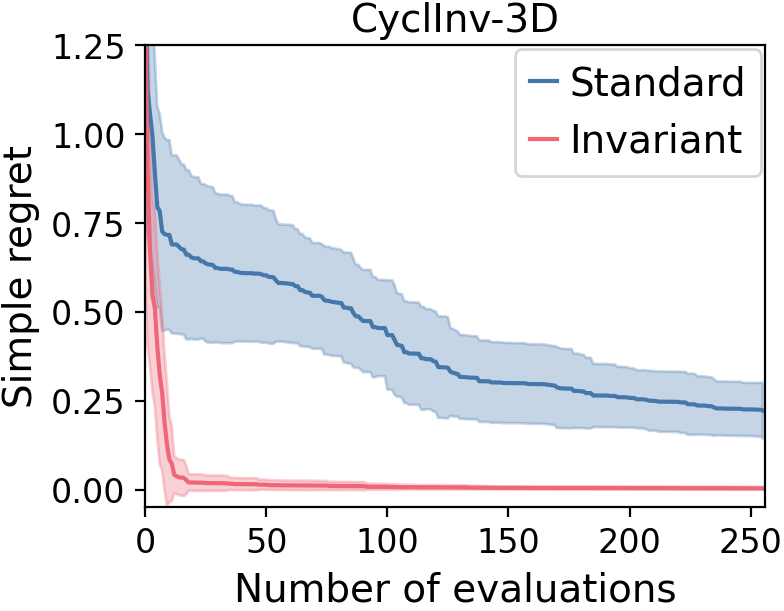
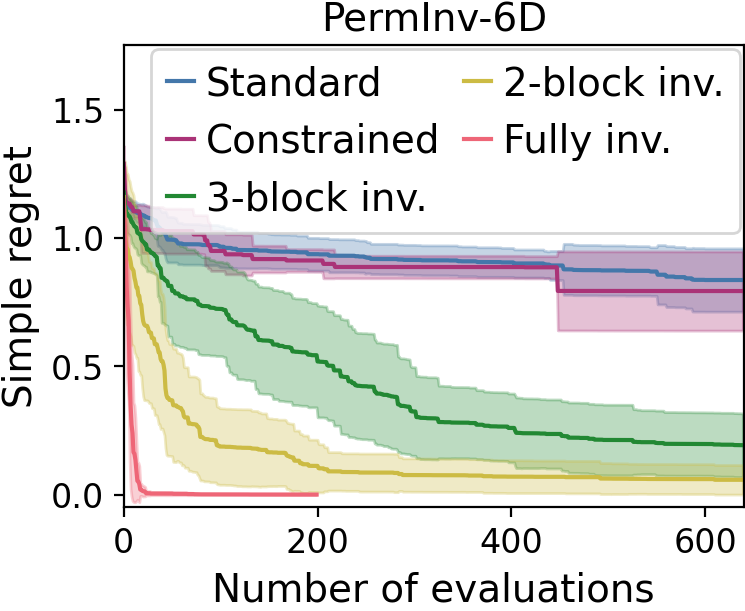
Invariant beats standard
Invariant beats constrained
Use subgroups for low-cost approximation (2- and 3- block invariance)

Application: fusion reactor design

High-temperature plasma → zero-carbon, low-waste energy

Task: find an operating point with high stability
Actuators are permutation invariant

Using an invariant kernel achieves better results!